【原学笔记】普攻回能机制与期望计算

结论速览：

t佬等人的《元素能量学》中，开篇即介绍了原神中角色的普攻、重击或瞄准射击在命中目标后，会有一个回能机制。

这里再复述一遍，涉及到接下来计算的条件用彩色字标出：

1.对应技能启动时，触发成功概率置为0.1(10%)

2.使用对应武器类型的角色，用普通攻击或蓄力攻击(弓角色的瞄准射击或其他角色的重击)攻击到敌人时，触发概率判断。

成功就进入回能控制，并将触发概率重新置为0.1(10%); 失败就给下一次判断的触发成功概率增加一定值。

*对于长柄武器，加0.04(4%)

*对于单手剑和弓，加0.05(5%)

*对于双手剑和法器，加0.1(10%)

3.在回能控制中，会按顺序检测角色的元素归属，然后对应角色固定回复1点能量。

*检测顺序为火，冰，雷，水，风，岩。

*回能控制的运行持续时间为0.2秒。也就是说相当于这个回能有个0.2秒的CD。

那么问题来了，每次攻击命中时，回能的期望值时多少呢？▌Part 1 数学原理介绍

可以发现，这个问题中，概率是会递增的，而且具有触发条件，需要把问题转化成一个马尔科夫链，这样就能满足状态转移矩阵的使用条件，从而得出结果。

不明觉厉，什么是“马尔科夫链”？

打个比方，

张三家门口有两家早餐店，A和B，如果张三前一天选择了A店，那么第二天有40%的概率选择B店，有60%的概率还是选择A店；如果张三前一天选择了B店，那么第二天有50%的概率选择A店，有50%的概率还是选择B店。

问，张三选择A、B店的平均概率是多少？

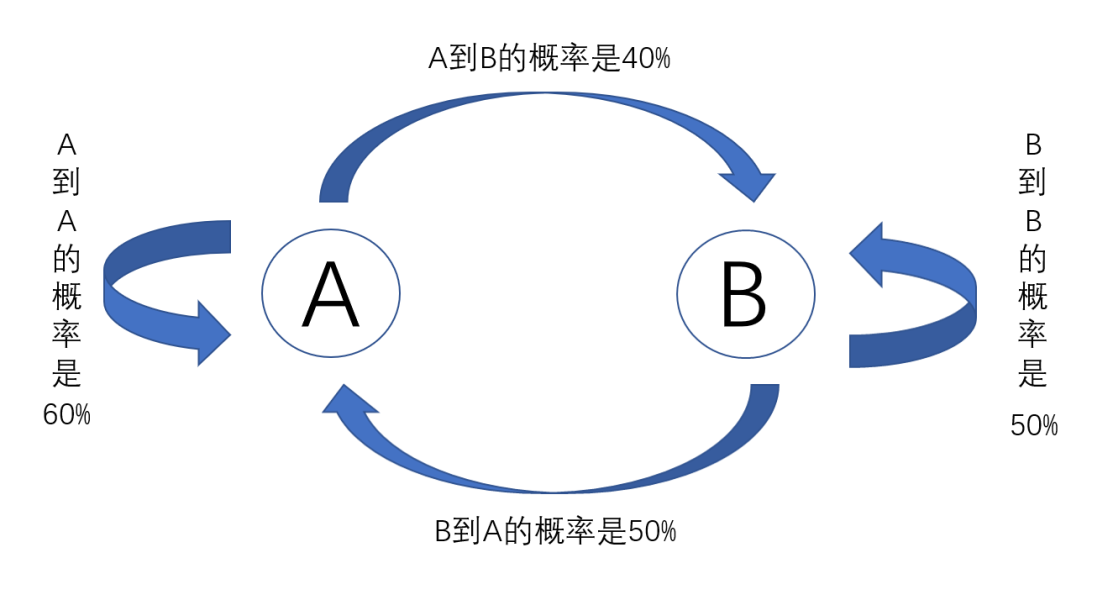
这就是一个马尔科夫链，用这样的图来表示。

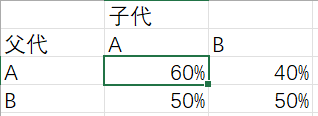
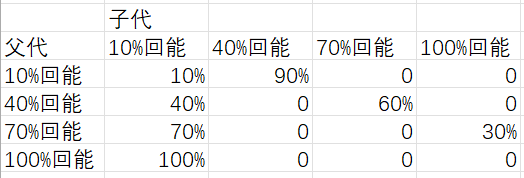
然后可以写出这样的表格，比如图中所选中的单元格就代表，从父代A到子代A的概率是60%。

对应：如果张三前一天选择了A店，第二天有60%的概率还是选择A店。

将这个表格的数据一一对应成矩阵中的元素，得到的就是所谓“状态转移矩阵”。

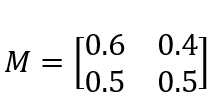
然后将这个矩阵M乘以一个向量（1,0），得到：

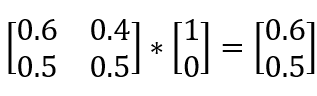
将得到的（0.6,0.5）再乘一遍矩阵M：

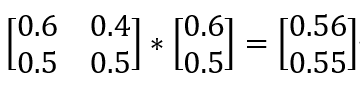
可以看到，所得矩阵的两个数值都越来越接近了，最后有：

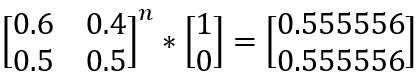
最终，张三选择A店的平均概率就约为55.56%

如果一开始乘的向量是（0,1），得到这个结果：

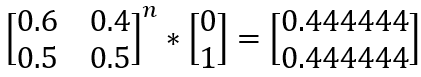
说明，张三选择B店的平均概率就约为44.44%

选择A店和选择B店的概率加起来正好是100%，成功归一，结果没有问题。

▌Part 2 简化问题模型

接下来解决普攻回能期望就只要照葫芦画瓢就行了，先画出这个问题的马尔科夫链，然后写出对应的状态转移矩阵，用一个初始向量多次乘以该矩阵，最后一定会得到一个稳定的值（这个问题肯定是收敛的），就是所要的结果了。

在此之前，再对原来的问题做一点简化：

1. 触发回能的基础概率是10%。

2. 假设本次没有触发回能，下次触发回能的概率提高30%。

3. 如果本次触发了回能，概率回到10%。

得到这张图：

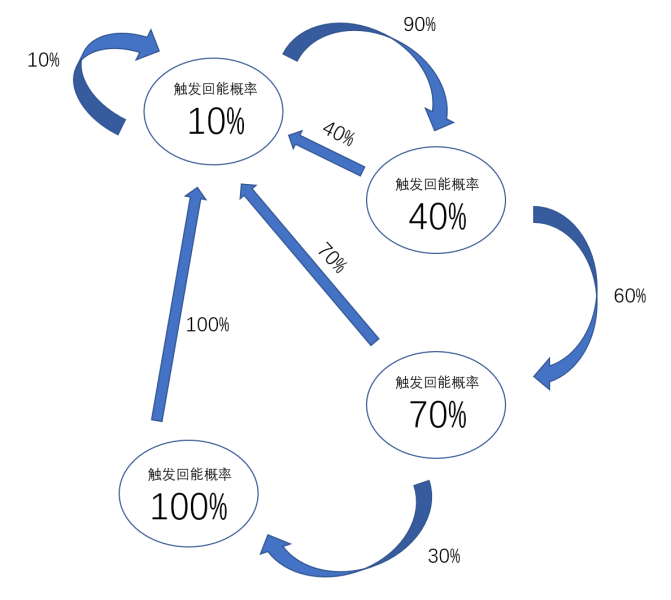
相应的矩阵也可以写出来了：

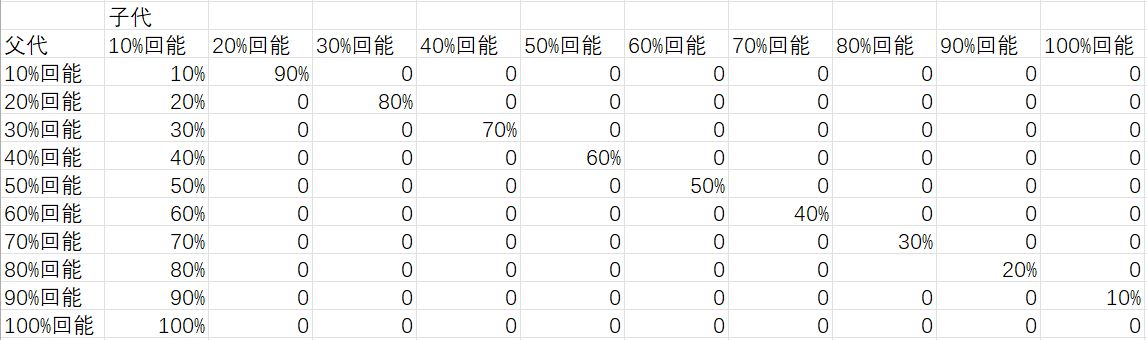
实际问题的矩阵也是张这个样子，只不过更大一点罢了。

▌Part 3 具体计算操作

先解出这种情况的，其它直接同理就行：

*对于双手剑和法器，加0.1(10%)

1.先把矩阵写出来

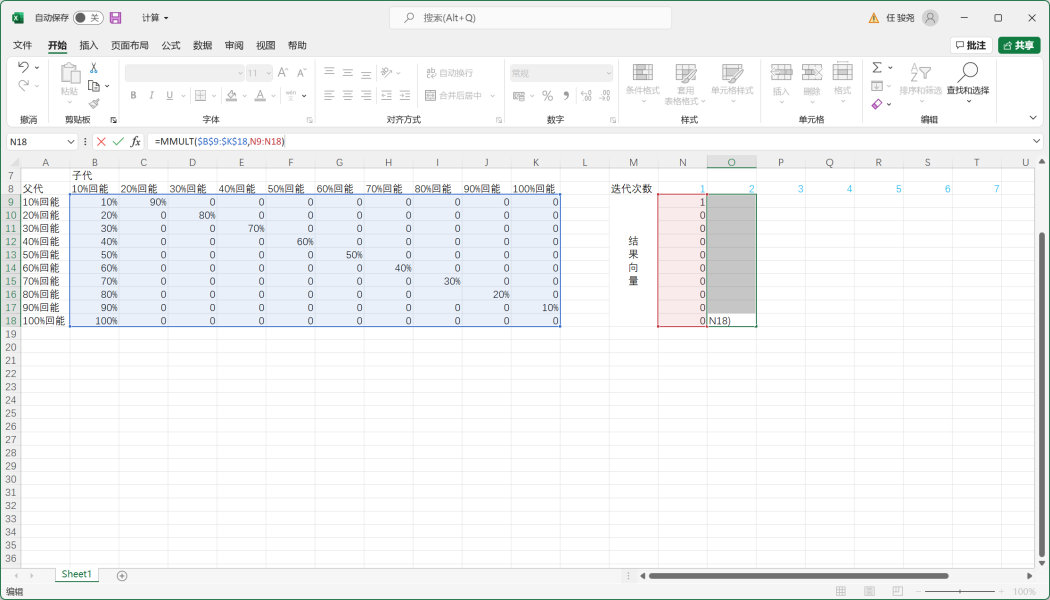
2.利用exl的MMULT函数，按照图中方法选定后，按Ctrl+Shift+Enter，即可得出结果向量。

3.把状态转移矩阵对应的单元格在公式中用美元符号$进行锁定后，按图中方法拖动格式刷。

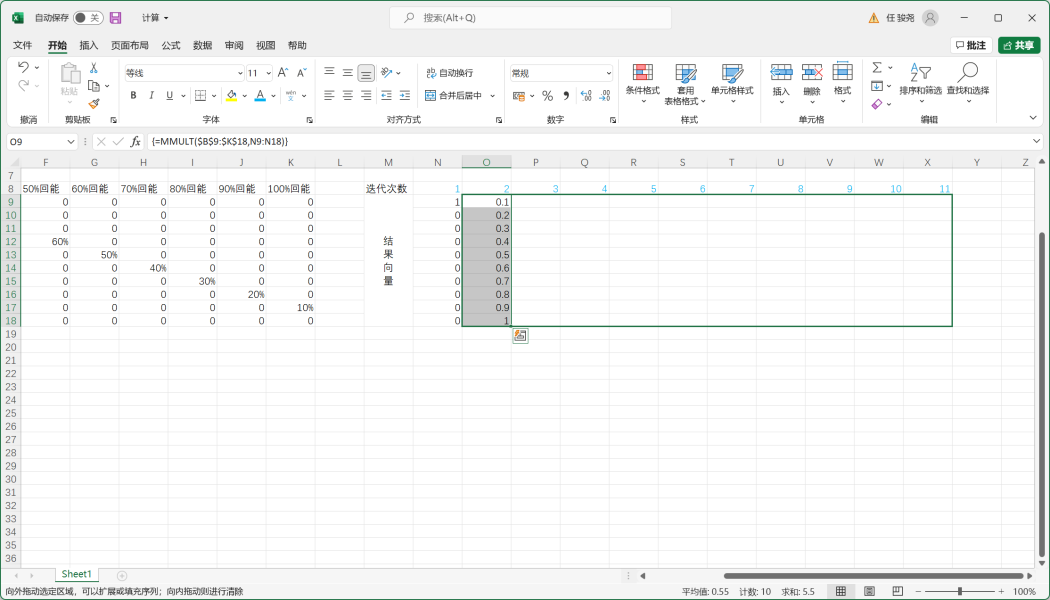
4.在迭代30次以后，得到了一个相对稳定的数据，这个就是双手剑和法器角色单次普攻回能的期望数值，0.273208

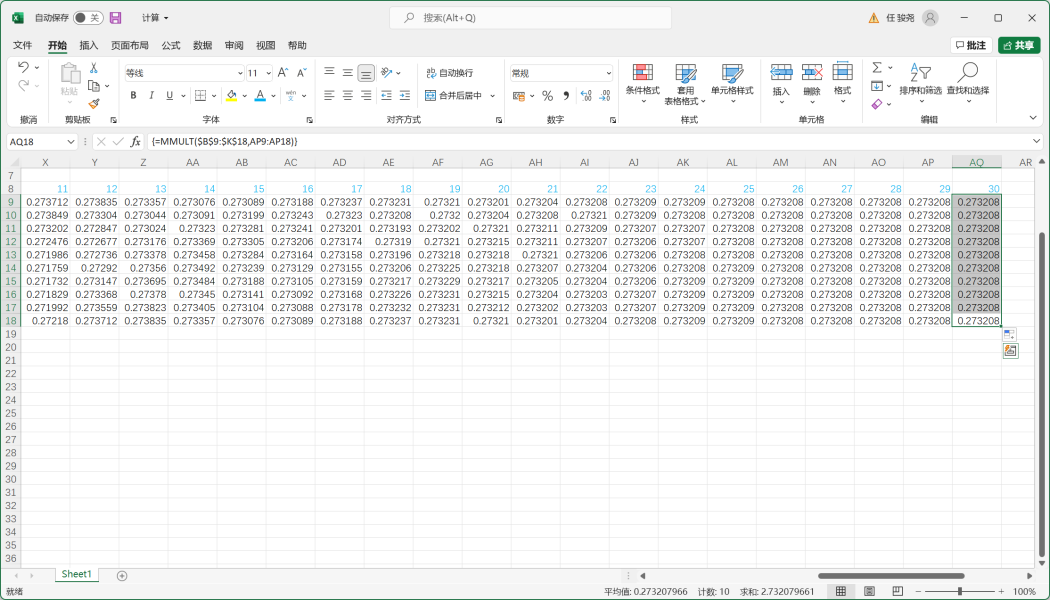
5.同理，得出其它类型角色的数据:

（精确到6位小数）

*对于长柄武器，单次普攻回能期望=0.207324

*对于单手剑和弓，单次普攻回能期望=0.221260

*对于双手剑和法器，单次普攻回能期望=0.273208

做了个图方便保存。

PS：用这个方法还可以解决

①宗室系列武器的收益问题

②明日方舟抽卡出货期望是34.594894抽

③原神的出货期望当然也可以算，就是1.6%。74抽以后就是这种概率递增