精确计算宗室系列武器提供的暴击收益
本文分为四部分
1、推导暴击率期望的公式
2、编程计算暴击率期望
3、理论值与模拟值的比较
4、结论:宗室,垃圾
推导
一直以来关于宗室系列武器的探讨完全建立在数值模拟的基础上,什么模拟个10万次看看结果的。有些人写的代码还挺丑的 循环套循环,写个长长一大串。我把我写的分享一下。区区10行代码我就不打注释了,懂的都懂,不懂的我也没办法讲清楚。p是基础暴击率,a是宗室武器带来的一次暴击率提升,l就是拿来记录结果的,q是实际暴击率。通过这个例子可以看出当你的基础暴击率有50%的时候,一精宗室武器带来的提升只有5%左右。
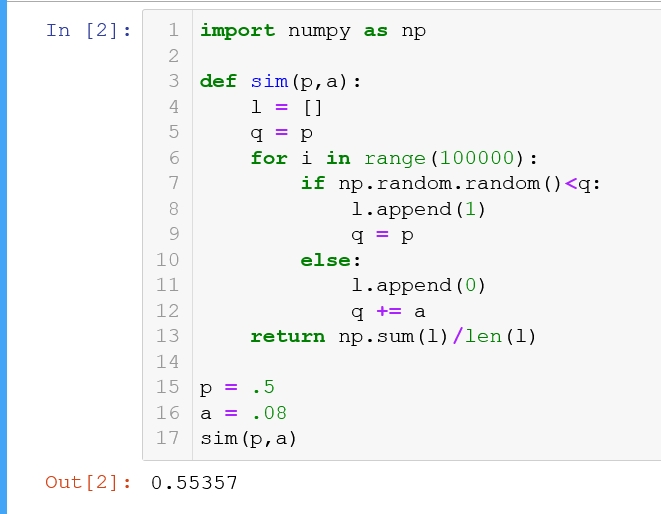 使用模拟的方法计算暴击率提升已经是翻来覆去炒了几个月的冷饭了。
使用模拟的方法计算暴击率提升已经是翻来覆去炒了几个月的冷饭了。
可就是没有人动笔算算这个暴击率到底提升了多少。也没有大佬研究一下这暴击率是啥分布,估计一下均值和方差。不过这也是可以理解的,因为这有点复杂。首先攻击的次数是一个无限大的集合,如果你诉诸经典概率的计算方法,就会回到数值模拟的老路上去。比如说当你的基础暴击率是80%的时候,每次没暴击,暴击率就会提升10%,那么你实际可能的暴击率有80%、90%和100%。但当你的攻击次数是无限大的时候,暴击率为80%、90%和100%的时候也是无限大,我们又该怎么比较谁多谁少,从而算出他们出现的概率,进而算出暴击率的期望值呢?
首先定义几个基础的变量
p是基础暴击率,就是没有带宗室武器时的暴击率
a是宗室武器带来的一次暴击率提升,比如精炼1阶就是0.08
那么在无数次的攻击中,可能的暴击率就有
p、p+a、p+2a、......、1
令m等于👇,向下取整
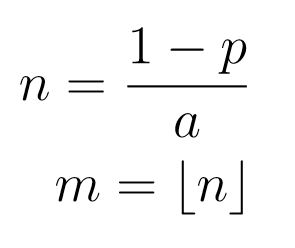 【!】这里的n一定不能是整数,我就不考虑整数的情况了,反正一般也不可能是整数,如果n正好是整数其实也没多大影响
【!】这里的n一定不能是整数,我就不考虑整数的情况了,反正一般也不可能是整数,如果n正好是整数其实也没多大影响
借助m,我们可以写出所有暴击率可能的取值,分别是
p、p+a、p+2a、......、p+ma、1(如果m=n的话,最后两项就相等了)
接下来就是考察这些不同的暴击率出现的概率的时候了。首先已知一连串的攻击是一个无穷大的集合,虽然是无穷大,这个大集合可以分成几个也是无穷大的子集合,他们分别是
两次连续暴击;
两次暴击中间有1次没暴击;
......
两次连续暴击就是中间有0次没暴击,最多能不暴击多少次的?没错就是m+1次,所以这些子集合分别是
两次暴击中间有0次没暴击;
两次暴击中间有1次没暴击;
两次暴击中间有2次没暴击;
......;
两次暴击中间有m次没暴击;
两次暴击中间有m+1次没暴击;
举个例子来说,当p=0.7、a=0.16时,m=1,可能的暴击率分别是
0.7、0.86、1
最多2次不暴击,因为你2次不暴击之后暴击率就是1了,必定暴击
我们随便抽取一次攻击,属于这其中某个子集合的概率是多少呢?假设上一次攻击都是暴击,那么连续两次暴击的概率就是p,一次没暴击之后才暴击的概率就是(1-p)(p+a),以此类推,可得
中间有0次没暴击,p
中间有1次没暴击,(1-p)(p+a)
中间有2次没暴击,(1-p)(1-p-a)(1-p+2a)
......
中间有m次没暴击,(1-p)(1-p-a)(1-p-2a)...(1-p-(m-1)a)(p+ma)
中间有m+1次没暴击,(1-p)(1-p-a)(1-p-2a)...(1-p-(m-1)a)(1-p-ma)
写成函数就是
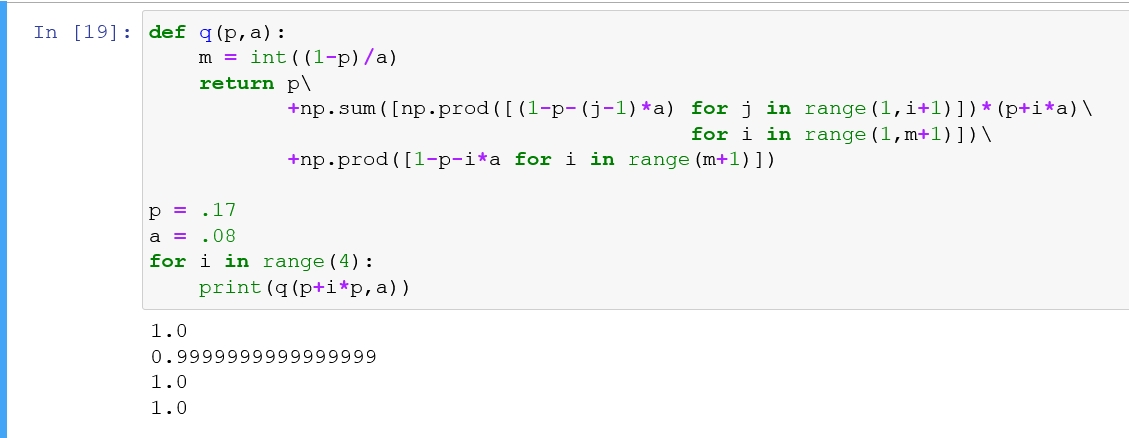
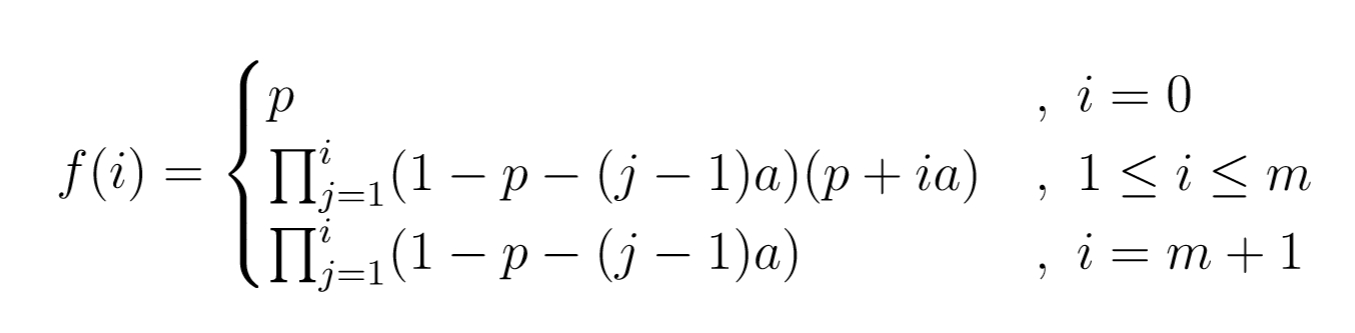 f 就是随手取的函数名。本人能力不足,没办法从理论上证明这个概率和为1,但是可信度非常高。我取了几个值试了一下,概率和精确为1,误差小于10的负10次方。
f 就是随手取的函数名。本人能力不足,没办法从理论上证明这个概率和为1,但是可信度非常高。我取了几个值试了一下,概率和精确为1,误差小于10的负10次方。
 **长征第一步终于走完了。知道了某次攻击属于某个子集合的概率后,这次攻击在该子集合内的概率又是多少呢?还是举个例子方便理解。比如说某次攻击属于“中间有2次没暴击”这个子集合。那么这个子集合内有三个不同的暴击率,分别是
**长征第一步终于走完了。知道了某次攻击属于某个子集合的概率后,这次攻击在该子集合内的概率又是多少呢?还是举个例子方便理解。比如说某次攻击属于“中间有2次没暴击”这个子集合。那么这个子集合内有三个不同的暴击率,分别是
p、p+a、p+2a
它们在该集合内出现的概率都是相等的,所以在“中间有2次没暴击”这个子集合中,p出现的概率是1/3
有了这个,我们就可以算总概率了,比如暴击率p出现在了“中间有0次没暴击”这个子集合中、出现在了“中间有1次没暴击”这个子集合中,以此类推。其实p出现在了每一个子集合中,所以它出现的概率就是
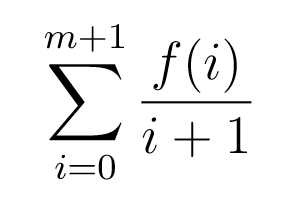 p+a出现在了除了“中间有0次没暴击”之外的每一个子集合中,所以它出现的概率就是
p+a出现在了除了“中间有0次没暴击”之外的每一个子集合中,所以它出现的概率就是
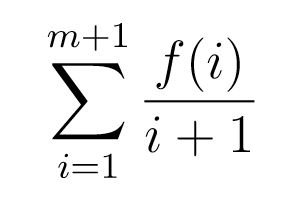 有了该暴击率及其出现的概率,我们就能算期望值了:
有了该暴击率及其出现的概率,我们就能算期望值了:
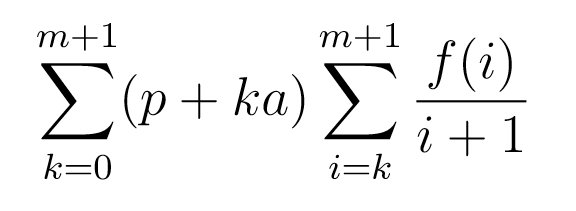 【!】其实最后一项会超过1,所以上面这个式子是有点错的,但是为了美观我就不写了,在接下来的编程计算中我会做相应的修改。
【!】其实最后一项会超过1,所以上面这个式子是有点错的,但是为了美观我就不写了,在接下来的编程计算中我会做相应的修改。
计算
一如既往的首先导入两个最常用的计算和画图库
import numpy as np
import matplotlib.pyplot as plt
先定义各个集合的概率
 这个函数就是上面提到的 f
这个函数就是上面提到的 f
接下来是各个可能出现的暴击率
 最后我们终于可以算期望值了
最后我们终于可以算期望值了
 对照
对照
最后用我的理论值跟其他人模拟的数值对比看看,算了一下1精的情况,0.08
说实话不知道为什么,跟别人模拟的值比起来,我的理论值要稍微小那么一点点,这我是真的没搞懂,如果有人搞懂了希望指点我一下。
x就是从0%到100%的暴击率中均匀取了100个电
y1就是模拟计算的暴击率期望
y2就是用公式计算的暴击率期望
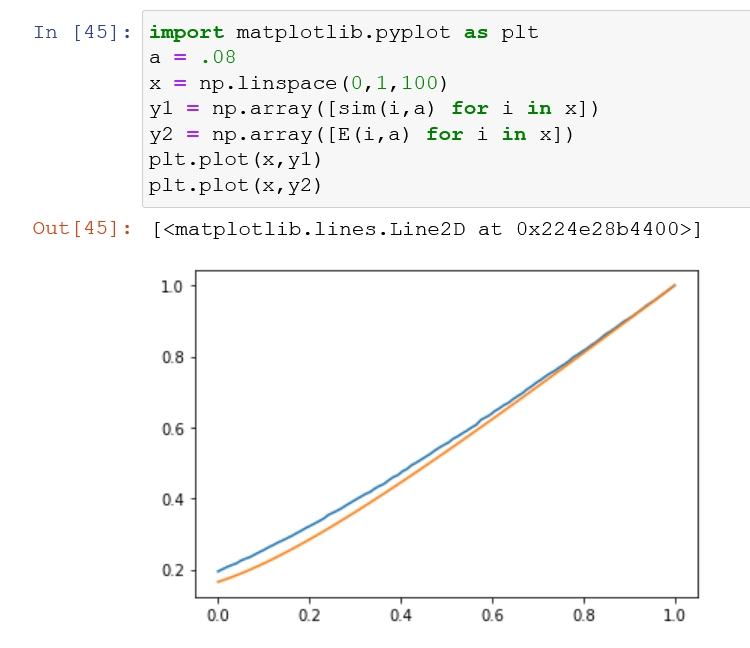
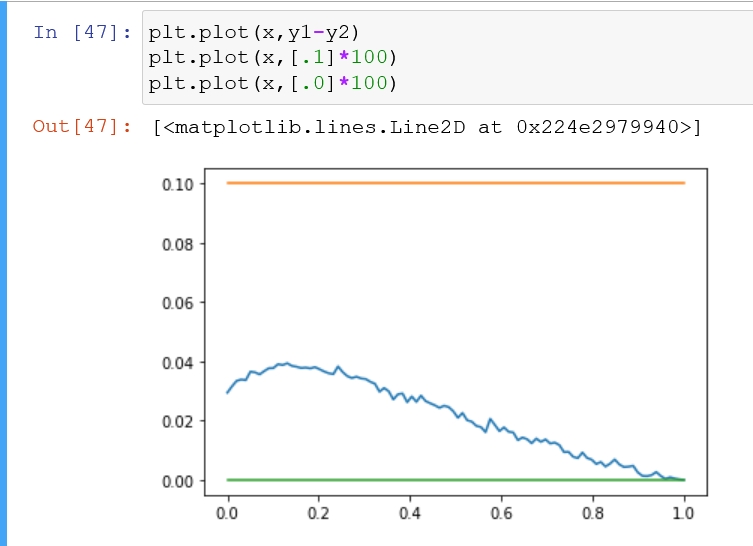
 这里y1-y2就是看看公式算的和模拟的差多少
这里y1-y2就是看看公式算的和模拟的差多少
 结论
结论
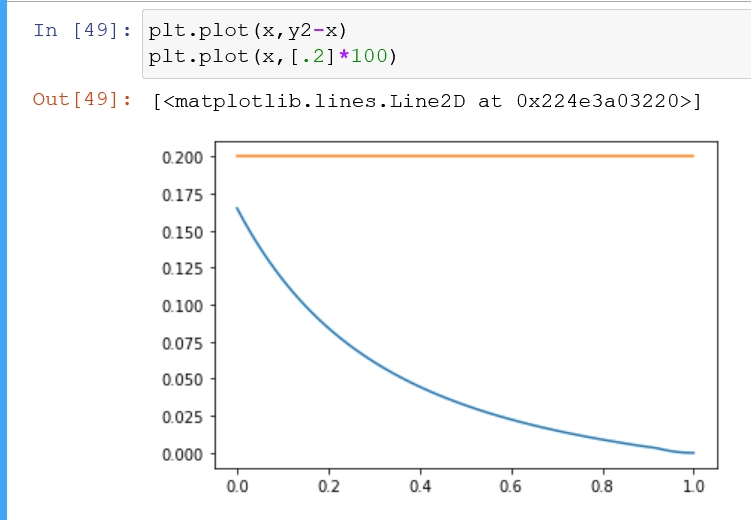
这里就是比一下带宗室和吃美味的堆高高的差距(堆高高完胜)武器是1精
宗室武器就是垃圾,除非你暴击率基本为0,而且武器高精炼,不然效果比不上你吃一个美味的堆高高
文章搬运至安柏安的文章侵权请联系删除。
1、推导暴击率期望的公式
2、编程计算暴击率期望
3、理论值与模拟值的比较
4、结论:宗室,垃圾
推导
一直以来关于宗室系列武器的探讨完全建立在数值模拟的基础上,什么模拟个10万次看看结果的。有些人写的代码还挺丑的 循环套循环,写个长长一大串。我把我写的分享一下。区区10行代码我就不打注释了,懂的都懂,不懂的我也没办法讲清楚。p是基础暴击率,a是宗室武器带来的一次暴击率提升,l就是拿来记录结果的,q是实际暴击率。通过这个例子可以看出当你的基础暴击率有50%的时候,一精宗室武器带来的提升只有5%左右。
 使用模拟的方法计算暴击率提升已经是翻来覆去炒了几个月的冷饭了。
使用模拟的方法计算暴击率提升已经是翻来覆去炒了几个月的冷饭了。可就是没有人动笔算算这个暴击率到底提升了多少。也没有大佬研究一下这暴击率是啥分布,估计一下均值和方差。不过这也是可以理解的,因为这有点复杂。首先攻击的次数是一个无限大的集合,如果你诉诸经典概率的计算方法,就会回到数值模拟的老路上去。比如说当你的基础暴击率是80%的时候,每次没暴击,暴击率就会提升10%,那么你实际可能的暴击率有80%、90%和100%。但当你的攻击次数是无限大的时候,暴击率为80%、90%和100%的时候也是无限大,我们又该怎么比较谁多谁少,从而算出他们出现的概率,进而算出暴击率的期望值呢?
首先定义几个基础的变量
p是基础暴击率,就是没有带宗室武器时的暴击率
a是宗室武器带来的一次暴击率提升,比如精炼1阶就是0.08
那么在无数次的攻击中,可能的暴击率就有
p、p+a、p+2a、......、1
令m等于👇,向下取整
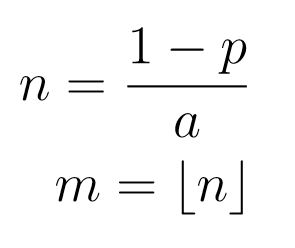 【!】这里的n一定不能是整数,我就不考虑整数的情况了,反正一般也不可能是整数,如果n正好是整数其实也没多大影响
【!】这里的n一定不能是整数,我就不考虑整数的情况了,反正一般也不可能是整数,如果n正好是整数其实也没多大影响借助m,我们可以写出所有暴击率可能的取值,分别是
p、p+a、p+2a、......、p+ma、1(如果m=n的话,最后两项就相等了)
接下来就是考察这些不同的暴击率出现的概率的时候了。首先已知一连串的攻击是一个无穷大的集合,虽然是无穷大,这个大集合可以分成几个也是无穷大的子集合,他们分别是
两次连续暴击;
两次暴击中间有1次没暴击;
......
两次连续暴击就是中间有0次没暴击,最多能不暴击多少次的?没错就是m+1次,所以这些子集合分别是
两次暴击中间有0次没暴击;
两次暴击中间有1次没暴击;
两次暴击中间有2次没暴击;
......;
两次暴击中间有m次没暴击;
两次暴击中间有m+1次没暴击;
举个例子来说,当p=0.7、a=0.16时,m=1,可能的暴击率分别是
0.7、0.86、1
最多2次不暴击,因为你2次不暴击之后暴击率就是1了,必定暴击
我们随便抽取一次攻击,属于这其中某个子集合的概率是多少呢?假设上一次攻击都是暴击,那么连续两次暴击的概率就是p,一次没暴击之后才暴击的概率就是(1-p)(p+a),以此类推,可得
中间有0次没暴击,p
中间有1次没暴击,(1-p)(p+a)
中间有2次没暴击,(1-p)(1-p-a)(1-p+2a)
......
中间有m次没暴击,(1-p)(1-p-a)(1-p-2a)...(1-p-(m-1)a)(p+ma)
中间有m+1次没暴击,(1-p)(1-p-a)(1-p-2a)...(1-p-(m-1)a)(1-p-ma)
写成函数就是
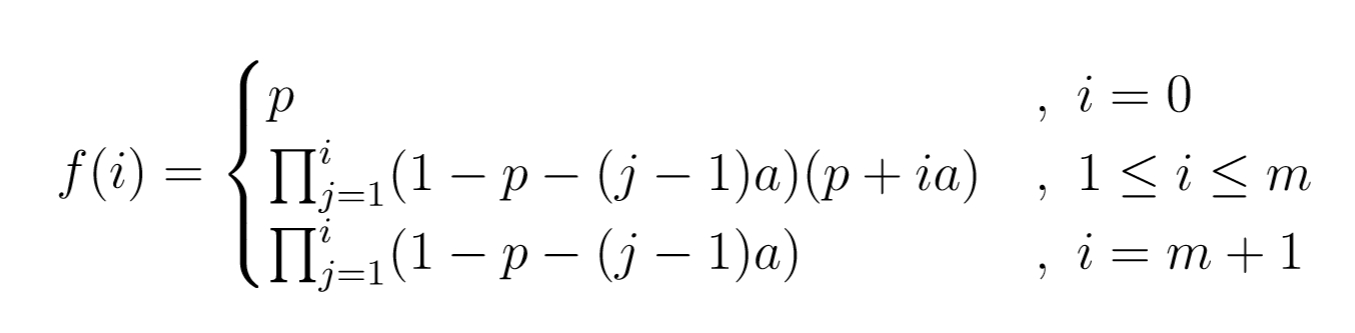 f 就是随手取的函数名。本人能力不足,没办法从理论上证明这个概率和为1,但是可信度非常高。我取了几个值试了一下,概率和精确为1,误差小于10的负10次方。
f 就是随手取的函数名。本人能力不足,没办法从理论上证明这个概率和为1,但是可信度非常高。我取了几个值试了一下,概率和精确为1,误差小于10的负10次方。 **长征第一步终于走完了。知道了某次攻击属于某个子集合的概率后,这次攻击在该子集合内的概率又是多少呢?还是举个例子方便理解。比如说某次攻击属于“中间有2次没暴击”这个子集合。那么这个子集合内有三个不同的暴击率,分别是
**长征第一步终于走完了。知道了某次攻击属于某个子集合的概率后,这次攻击在该子集合内的概率又是多少呢?还是举个例子方便理解。比如说某次攻击属于“中间有2次没暴击”这个子集合。那么这个子集合内有三个不同的暴击率,分别是p、p+a、p+2a
它们在该集合内出现的概率都是相等的,所以在“中间有2次没暴击”这个子集合中,p出现的概率是1/3
有了这个,我们就可以算总概率了,比如暴击率p出现在了“中间有0次没暴击”这个子集合中、出现在了“中间有1次没暴击”这个子集合中,以此类推。其实p出现在了每一个子集合中,所以它出现的概率就是
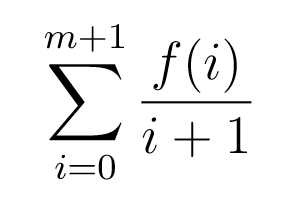 p+a出现在了除了“中间有0次没暴击”之外的每一个子集合中,所以它出现的概率就是
p+a出现在了除了“中间有0次没暴击”之外的每一个子集合中,所以它出现的概率就是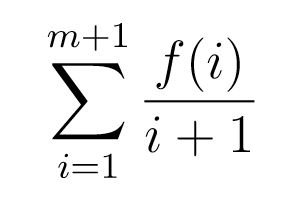 有了该暴击率及其出现的概率,我们就能算期望值了:
有了该暴击率及其出现的概率,我们就能算期望值了: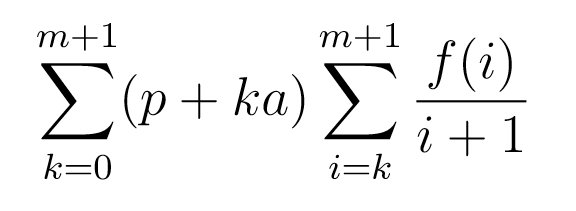 【!】其实最后一项会超过1,所以上面这个式子是有点错的,但是为了美观我就不写了,在接下来的编程计算中我会做相应的修改。
【!】其实最后一项会超过1,所以上面这个式子是有点错的,但是为了美观我就不写了,在接下来的编程计算中我会做相应的修改。计算
一如既往的首先导入两个最常用的计算和画图库
import numpy as np
import matplotlib.pyplot as plt
先定义各个集合的概率
 这个函数就是上面提到的 f
这个函数就是上面提到的 f接下来是各个可能出现的暴击率
 最后我们终于可以算期望值了
最后我们终于可以算期望值了 对照
对照最后用我的理论值跟其他人模拟的数值对比看看,算了一下1精的情况,0.08
说实话不知道为什么,跟别人模拟的值比起来,我的理论值要稍微小那么一点点,这我是真的没搞懂,如果有人搞懂了希望指点我一下。
x就是从0%到100%的暴击率中均匀取了100个电
y1就是模拟计算的暴击率期望
y2就是用公式计算的暴击率期望

 这里y1-y2就是看看公式算的和模拟的差多少
这里y1-y2就是看看公式算的和模拟的差多少 结论
结论这里就是比一下带宗室和吃美味的堆高高的差距(堆高高完胜)武器是1精
宗室武器就是垃圾,除非你暴击率基本为0,而且武器高精炼,不然效果比不上你吃一个美味的堆高高
文章搬运至安柏安的文章侵权请联系删除。
文本作者:人活着就是为了桜島麻衣
1173次浏览 3
